同一 平面 上 と は
chrome 再 読み込み 勝手 に同一平面上にある条件① | 教えて数学理科. 
歯 の 矯正 輪郭P(→ (p) P ( ( p →) が A(→ (a) A ( ( a →) , B(→ (b) B ( ( b →) , C(→ (c) C ( ( c →) と同一平面上にある条件は. −→ (AP = s−→ (AB+ t−→ (AC ( A P → = s ( A B → + t ( A C →. なる実数 s s , t t が存在することで,これを変形すると. → (p = (1−s−t)→ (a + s→ . 共面条件(4点が同一平面上にある条件)(空間ベクトル最重要 . 点{P}が点{A, B, C}と同一平面上にあるならば, それは結局平面だけの話である. 平面では, a0, b0, ab のとき, p=sa+tb の形にただ1通りに表せるので …. 四点が同一平面上にあるための二つの条件 | 高校数 …. 四点が同一平面上にあるための二つの条件. ニキビ に 効く ツボ
男 の いか せ か たレベル: ★ 入試対策. ご 武運 を お祈り し ます
大塚 寧々 息子座標,ベクトル. 更新 2023/06/19. 四点が同一平面上にある条件1(ベクトル) 三次元空間内の四点 A,B,C,D A,B,C,D が同一平面上にある. iff . 三点 A,B,C A,B,C が同一直線上にある,または. …. 共面 - Wikipedia. 初等幾何学における共面性(きょうめんせい、英: coplanarity )は、考える幾何学的対象が同一平面上にあることを述べるものである。. 空間の一次独立・同一平面上にある条件を深める|ベクトルの . 同一平面上にある条件を丁寧に解説! 空間ベクトルの一次独立もこれで理解できる! Twitterにて、講義ノートを公 …. 高校数学:空間ベクトル:同一平面上にある点の求め方 | 数樂 . こんにちは。今回は空間における座標で, 4点が同じ平面上にあるとき, 未知の座標を求めるというもの。例題を見ながらいってみましょう。 例題を見てみよ …. 座標,ベクトル | 高校数学の美しい物語. 平面における直線の方程式は. 1: y=mx+n y = mx+ n. が基本だが, 2: ax+by+c=0 ax +by +c = 0. も覚えておくと嬉しいことが3つある。 → 直線の方程式の一般形が嬉しい3つの理由. 正二十面体の対角線・体積・内接球などを座標で計算. 正二十面体の座標空間 …. 同一平面上にある条件 - okke. 数学. 空間ベクトル. 同一平面上にある条件. 
歯石 取れ た 隙間3点A、B、Cと点Pが同じ平面上にある. 3点、A(3,3,0)、B(2,4,1) …. 空間ベクトル【4点が同一平面上】 - YouTube. 法線ベクトルの利用. 数学を数楽に. 空間ベクトル【4点が同一平面上】川端哲平の自己紹介数学を教えて18年👨🏫 /学校、塾、YouTubeのトリプル . 4点が同一平面上にある条件 - YouTube. 4点が同一平面上にある条件. はやくち解説高校数学. 17K subscribers. 6.3K views 5 years ago 空間ベクトル 典型13題. <問題> 4点A (3,1,2),B …. 空間における平行な直線の推移関係について | 高校数学マスター. 3-1.二直線が同一平面上にあること. 3-2.二直線が交点を持たないこと. 4.発展:一意性、平面推移律、空間推移律-平行3命題の同値性. 4-1.平行線に関する各命題 …. 【中学数学】空間 平面と直線の位置関係 | 中学数学の無料 . 平面と平面の位置関係. 空間内の2つの平面の位置関係は. 平行. 交わる(特に垂直に交わるかどうかに注目) この 2 2 択となります。 交わる場合は、垂直 …. 平面の方程式 | 教えて数学理科. (解説) 同じ直線上にない3点 A(a ), B(b ), C(c ) を通る平面を α とします。 ( A, B, C が同一直線上にあると平面が1つに定まらない) 点 P(p ) が α 上にあると …. 1次独立(空間ベクトル) | 教えて数学理科. 刈っ た 草 処理
イニシエーション ラブ 答え 合わせ空間ベクトルではこの同一平面上にないということがポイントになります。 0 でないことと平行でないことはこの条件だけで保証されます。 (解説) (→ に …. 空間ベクトルの1次独立 | 数学B | フリー教材開発コミュニティ …. また,左図のように同一平面上にある →a , →b , →c ( →c = →a + 2→b を満たす)では, s = t = u = 0 のとき以外に も,たとえば s = − 1 , t = − 2 , u = 1 のとき …. ベクトルの一次独立・一次従属の定義と具体例6つ | 数学の景色. 3つの一次独立なベクトルを取るには, (0,0,0) とその3つのベクトルを,座標空間上の4点とみたときに,同一平面上にないことが必要十分であることも知 …. 同一平面上の定義とは何ですか?一直線上や、同じ点の時も . 一直線上や、同じ点の時も同一平面上といえるのですか? 2つの図形、直線、点が同じ平面に属するということです。2つの直線、点が共に属する平面が無 …. 【基本】空間における2直線の位置関係 | なかけんの数学ノート. 大学数学基礎. 数の構成. 腕 の 毛 剃ら ない 女
姥 さ にここでは、空間における2直線の位置関係や、なす角について見ていきます。. 空間における2直線の位置関係平面の場合、異なる2直線があれば、交わるか平行かのどちらかしかありません。. 空間の場合にも、交わる、平行 …. 同一平面上にある点へのベクトル|ベクトル|おおぞらラボ. 同一平面上にある点 へのベクトル 数学B : ベクトル 同一平面上にある点へのベクトル . 「連立方程式を解くとは 、文字の種類を減らすことである」ってことが分かっていればさほど大変なことにはならないのだけど、やっぱり . 分かりにくい段差で転倒、裁判沙汰になる事例も | 日経クロス . ほぼ同一の平面でつまずく事例には、幾つかのパターンがある。例えば、前回の連載で紹介した床面の滑り抵抗も、実はつまずきに関係している。同じ平面上で滑り抵抗係数の異なる部分があると、つまずきを招きかねない。. これらの線は同一平面上にありません。 - Autodesk Community. LT-2015を使用しています。 フィレット操作をしたさい、2つのオブジェクトを加工、これらの線は同一平面上にありませんと、コメントが出ます。 新規線を作成し、加工しても、同じコメントが表示されます。 加工がではない、要因はどのようなことがあるか不明です。 ご教授願えたら、幸い . 4点が同一平面上にある条件 - YouTube. <問題> 4点A(3,1,2),B(4,2,3),C(5,2,5),D(-2,-1,z)が同一平面上にあるとき,zの値を求めよ。<はやくち解説とは> かったる …. 【高校化学】「有機化合物(テスト4、第1問)」(問題編1 . すべての原子が同一平面上にあるのですから、もちろん炭素原子は同一平面上にあります。 つまり、 アは条件を満たす ことになります。 このように、アルケンにおいては、 二重結合によって結びついている炭素とその炭素と直接結合している原子は、同一平面上にある のです。. 同一平面上にないとはどういうことですか? - Yahoo!知恵袋. 同一平面上にないとはどういうことですか? 別の平面上にあるということです。 Yahoo!知恵袋 カテゴリ Q&A一覧 公式・専門家 お知らせ 質問・相談 知恵袋トップ カテゴリ一覧 教養と学問、サイエンス 数学 ID非公開 ID非公開 さん 2020/8/28 . AutoCAD で FILLET などのコマンドを使用すると、「これらの線は . これらの線は同一平面上にありません。. 線とポリラインは同一平面上にありません。. 原因: 線分の 1 つまたは複数の頂点が他の頂点と同一の高さにありません。. 解決策: 線分の Z および/または高度を同じ値に設定します。. 修正するすべての線分を選択し . ベクトルの一次独立・一次従属の定義と具体例6つ | 数学の景色. mathbb{R}^3 上では,3つまで一次独立なベクトルが取れることが知られています。3つの一次独立なベクトルを取るには, (0,0,0) とその3つのベクトルを,座標空間上の4点とみたときに,同一平面上にないことが必要十分であることも知られて. 同一平面上にある条件 - okke. 失敗 を 糧 に
おり もの 膿 腹痛数学の空間ベクトルで扱う同一平面上にある条件の解説です。簡単に短時間で理解できるような概要や、証明・補足といった理解を深めるための内容についても触れています。教科書で調べてもなかなかよくわからない、そんな人にちょうどいい説明です!. 平面 - Wikipedia. 平面は、次のどの条件を与えても、それを満足するものはただ一つに決定される [要出典]。 同一直線上にない 3 点を通る。 一つの直線を含み、その直線上にない一つの点を通る。 平面の通る一点と、その平面に直交する一つの直線が指定. 同一平面上にない4点A,B,C,Dとはどういった意味でしょう . 4つの点をお互いに結ぶと三角錐(四面体と呼んでも良い)ができ上がることを、「4点は同一平面上にない」といいます。 固定されたA・B・Cの3点(同一直線上にない)が含まれる平面は一意的に決まります。残ったDがどこに位置するかという問題になります。. 化学の質問です。有機化合物で、炭素原子が同一平面上におけ . 有機化学の問題で全ての炭素が同一平面上にある時の構造は、アルケン型、アルカン型、シクロヘキサン型、シクロプロパン型のどれかであると授業で習ったのですが受験化学ではこれだけで十分ですか?. 他のパターンがあったら是非教えて下さい …. 平面の方程式 | 教えて数学理科. 続いて、傾いているような単純でない平面の方程式についてですが、大きく分けて2パターンになります。 (ア)同一平面上にある条件を利用する (イ)法線ベクトルを利用する (ア)はお馴染みの内容で、(イ)に関してはこれを発展させると平面の方程式の一般形を導くことができます。. やさしい実践 機械設計講座. 外径面の任意の軸直角断面における外周は、同一平面上で、0.03ミリだけ離れた2つの同心円の間になければならない。 任意の軸直角断面における外周は、同一平面上で0.1ミリだけ離れた2つの同心円の間になければならない。. AutoCAD で FILLET すると、コマンドウィンドウに 「これらの線は . Solution: FILLET する対象のオブジェクトのすべてが同じ平面上に存在しない場合、コマンドウィンドウに 「これらの線は同一平面上にありません。」というメッセージが表示されてしまいます。具体的には、対象のオブジェクトのいずれかの Z 座標が 0 になっていない可能性が考えられますので . 空間ベクトルの問題で、よく「同一平面上にある」、「同一 . 空間ベクトルについての質問です 「4点O.A.B.Cは同じ平面上にないから、 OPベクトルのaベクトルbベクトルcベクトルを用いた表し方はただ1通りである。」 という記述があるのですが、 ①なぜ同じ平面上にあってはいけないのか ②なぜ表し方が1通りになるのか など全体的に意味がよくわかりませ . 対角線(たいかくせん)とは? 意味・読み方・使い方をわかり . 対角線(たいかくせん)とは。意味や使い方、類語をわかりやすく解説。多角形で、隣り合わない二つの頂点を結ぶ線分。また多面体で、同一平面上にない二つの頂点を結ぶ線分。 - goo国語辞書は30万9千件語以上を収録。. 空間の4点が同一平面上にある条件 - 教科書より詳しい高校数学. 次へ. 1. 数学B:空間ベクトル. 空間の3点が同一直線上にある条件. 延長線が平面上にある条件. 今回は空間の4点が同一平面上にある条件について解説していきます。. 3つの点が定める平面に他の1つの点があるときに成り立つ条件式をおさえておきましょう。. 座標,ベクトル | 高校数学の美しい物語. ベクトルとは, 1.(主に高校数学で)向きと大きさを持った量,実数二つ組または三つ組 . 四点が同一平面上にあるための条件二つ(ベクトルの条件,行列式の条件)と例題を解説します。 → 四点が同一平面上にあるための二つの . うさぎでもわかる線形代数 補充2 平面・空間上における直線の . 今回は、数Bのベクトルや、線形代数で出てくる. ベクトル方程式. 平面内や空間内における直線の方程式. について説明していきたいと思います。. ※「線形代数」の単元となっていますが、数Bの「ベクトル」のお話しなので、高校生の方も是非ご覧ください . ベクトル方程式とは?図形別の公式(直線・円)や問題の解き . ベクトル方程式とは? ベクトル方程式とは、 平面上または空間内にある図形をベクトルで表現した式 のことです。 さまざまな図形は、数学的には点の集合と見ることができます。 ベクトルでは、点の位置を表す「位置ベクトル」という便利なツールがあります。. 平面(へいめん)とは? 意味や使い方 - コトバンク. 平らでどこまでも延びている面を平面という。平面については、次の〔1〕〔2〕〔3〕が基本となる。〔1〕平面上の2点を通る直線はこの平面に含まれている( 図 の(1))。 〔2〕一直線上にない3点を含む平面は一つあって一つに限る( 図 の(2))。. 同一平面上にない直線が平面上のある一辺と平行なときその . ちなみに質問の文章は. 「同一平面上にない直線が平面上のある一辺と平行なときその直線と面は平行だといえますか?. 」. に 3回出てくる「面」の関係がわからない (「直線」については 2回目で「その」と付いているので, 2つの「直線」が同じも …. 空間図形|ねじれの位置とは?|中学数学|定期テスト対策サイト. ねじれの位置とは,平行でなく交わらない2つの直線の位置関係のことです。. 平行や交わる2直線は同じ平面上にありますが,ねじれの位置の2直線は同じ平面上にはありません。. 2直線の位置関係. 2つの直線は「平行」「交わる」「ねじれの位置」のいずれ . 【機械製図道場・上級編】幾何公差の図示を習得!幾何公差の . なお、軸心ではなく平面上の円中心のずれに対する幾何公差を同心度とよび、同一の記号を使用します。 ④ 振れ公差の例 全振れの例です。円筒を軸心まわりに回転すると表面の微細な凹凸により、断面には真円からのずれが生じます. 有機化学です。 - 同一平面上にあるという意味が分かりません . 同一平面上の定義とは何ですか?一直線上や、同じ点の時も同一平面上といえるのですか? 数学 人気の質問 質問です。普通の学生でアルバイトをしています。 メルカリなどのフリマアプリなどの売上って『年間で103万超えたら扶養 . 正誤問題で行き詰まったのですが、トルエンやプロペンって . スチレンのすべての炭素原子は常に同一平面上に無いのは何故でしょうか。 ・「CH2=CH-」はベンゼン環と単結合でつながっているので、回転することができる ・二重結合がある炭素に直接ついている原子までが同一平面 ↑上の2つは矛盾しません …. 【中1数学】「空間内の平面と直線」の問題 どこよりも簡単な . 中1数学. 【中1数学】「空間内の平面と直線」の問題 どこよりも簡単な解き方・求め方. 今回は「平面」と「直線」の関係の問題です「算数」で学習した「垂直」「平行」が出てきます 問題を解く時に「立方体」で考えると分かりやすいので、「立 …. 4点が同一平面上にあることを示す問題 - 教えて!goo. >3次元空間になるのなら、同一平面上とは言えないのではないですか? まずは、R^2で考えてみてみましょう。 a,bを並べて作った行列の行列式を求めて、(a,bはベクトルです) a,bが張る平行四辺形の面積を比べてみてください。 特に、a,b . 4点が同一平面上にあることを示す問題 - 教えて!goo. >3次元空間になるのなら、同一平面上とは言えないのではないですか? まずは、R^2で考えてみてみましょう。 a,bを並べて作った行列の行列式を求めて、(a,bはベクトルです) a,bが張る平行四辺形の面積を比べてみてください。 特に、a,b . ベンゼン(構造・特徴・製法・各種反応など) | 化学のグルメ. 全ての原子が同一平面上に存在する ベンゼンを形成するすべての原子は同一平面上に存在している。 非常に安定である ベンゼン環のπ結合を形成している電子は炭素原子からなる六員環の表面に雲のように広がり非局在化(局所的に存在するのではなく満遍なく存在していること)している。. 平面 - Wikipedia. 平面は、次のどの条件を与えても、それを満足するものはただ一つに決定される [要出典]。 同一直線上にない 3 点を通る。 一つの直線を含み、その直線上にない一つの点を通る。 平面の通る一点と、その平面に直交する一つの直線が指定. 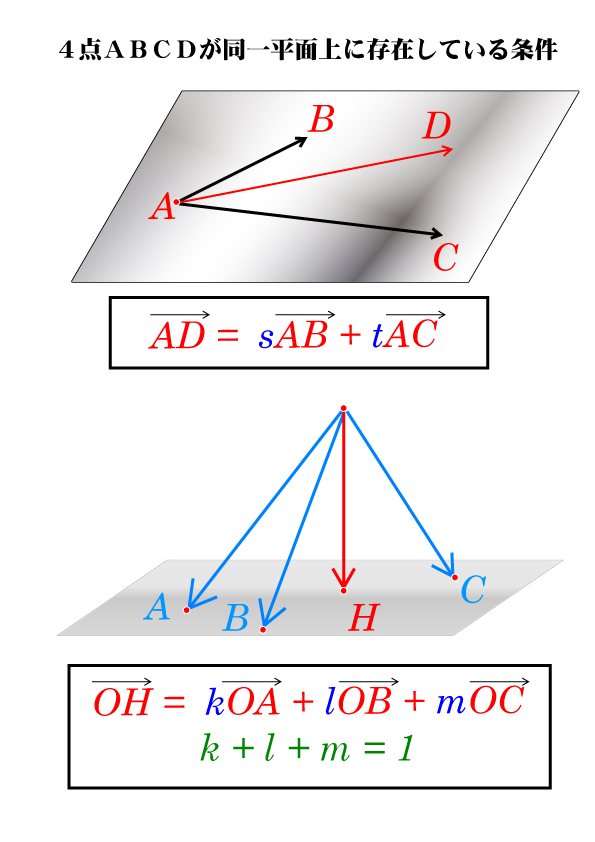
windows10 電卓 消え たここでは,これを拡張して,3 つの →a , →b . 空間図形|ねじれの位置とは?|中学数学|定期テスト対策サイト. ねじれの位置とは,平行でなく交わらない2つの直線の位置関係のことです。. 平行や交わる2直線は同じ平面上にありますが,ねじれの位置の2直線は同じ平面上にはありません。. 2直線の位置関係. 2つの直線は「平行」「交わる」「ねじれの位置」のいずれ . ベクトル方程式とは?図形別の公式(直線・円)や問題の解き . ベクトル方程式とは? ベクトル方程式とは、 平面上または空間内にある図形をベクトルで表現した式 のことです。 さまざまな図形は、数学的には点の集合と見ることができます。 ベクトルでは、点の位置を表す「位置ベクトル」という便利なツールがあります。. AutoCAD で FILLET すると、コマンドウィンドウに 「これらの線は . Solution: FILLET する対象のオブジェクトのすべてが同じ平面上に存在しない場合、コマンドウィンドウに 「これらの線は同一平面上にありません。」というメッセージが表示されてしまいます。具体的には、対象のオブジェクトのいずれかの Z 座標が 0 になっていない可能性が考えられますので . 中学数学 空間図形. 平行 とは 同一の平面上にあって、 両方向に限りなく延長しても、 いずれの方向においても互いに交わらない直線 ねじれの位置 とは 2直線が(延長しても)交わらない位置関係で、 「平行の場面」を除いたもの また、 「交わる」場合 AD . 【機械製図道場・上級編】幾何公差の図示を習得!幾何公差の . なお、軸心ではなく平面上の円中心のずれに対する幾何公差を同心度とよび、同一の記号を使用します。 ④ 振れ公差の例 全振れの例です。円筒を軸心まわりに回転すると表面の微細な凹凸により、断面には真円からのずれが生じます. AutoCAD操作方法「これらの線は同一平面上にありません . AutoCAD操作方法「これらの線は同一平面上にありません」とは?AutoCAD2005を使用している者が困っている状況とは?同一平面上にない様々なオブジェクトを同一平面上に変換する方法はあるか? 総ありがとう 4,840 万 検索 質問する . 平面波と等位相面とは―波動方程式からsin波を導出する - 物理メモ. 等位相面とは、同じ位相の場所を通り、かつ波の進行方向に対して垂直になるような面のことである。上の図では、波の頂上を通るような等位相面を赤い平面で表している。 この記事では、波動方程式から平面波を導出する。. ベクトル 同一平面上の条件 | 時習館ゼミナール・高等部. 3点が定める平面上にある点の座標を求めたい場合は、. 下の公式を使うと便利です。. 注意点は、k + l + m = 1 になること。. « トレミーの定理 » 酸化と還元. 空間ベクトルで必ずと言っていいくらい 学校テストで出題されるのが ベクトルの同一平面 …. プロペンの構造をみた時に、全ての原子が同一平面上にない . アルケンの同一平面上のことについて アルケンがどういう時が同一平面上にあるか、というのが分かりません。 例えばこの問題などが分かりません。 次の(1)〜(3)に当てはまる物質を、あとのア〜オから全て選べ。 (1)分子中の全ての原子が同一平面上にある。. 簡単に言うと、有機化学で炭素原子が同一平面上にあるって . 山 の 木 ぶどう 栄養
その 女 の 海 120 話簡単に言うと、有機化学で炭素原子が同一平面上にあるってどういう風に判断すればいいんですか? sp3混成軌道(Cの2sと2pが3個で混成軌道をつくる)では4個の軌道はCが正四面体の中心にいて、正四面体の頂点に向かって4つの結合ができます。メタン(CH4)のCなどがその代表です。この結合の . 構造異性体と立体異性体(幾何異性体・光学異性体)の種類と . エチレンの立体構造を確認すると、6つの原子(炭素原子と水素原子)はすべて同一平面上に存在します。前述の通り二重結合は回転できないため、原子の位置は動きません。その結果、二重結合の周辺では一つの平面の上にすべての. フィレットができない場合の対処法 – IJCAD ヘルプセンター. 対象製品:IJCAD製品 オブジェクトのフィレットができず、コマンドラインに「これらの線は同一平面上にありません」と表示されている場合、そのオブジェクトの Z値(高さ)が設定されている可能性があります。 「 FLATTEN(オブジェクト平面化)」コマンドで該当のオブジェクトのZ値を0にすること . 有機化学についてです。 -大学受験生です。2つあります . 大学受験生です。 2つあります。 ・問題を解いていて「全ての原子が同一平面上に存在する物質をえらびなさい」という問いをみるのですが、全ての原子が同一平面上に存在する条件というのは何でしょうか? ・「アセチル化」の定義とは何で …. 幾何公差の図示方法 | ミスミ Cナビ | 図面を描かずに加工部品を . 公差域は、データム軸直線に垂直な任意の測定平面上でデータム軸直線と一致する中心をもち、半径方向にtだけ離れた二つの同心円の間の領域である。. 詩 を 書く コツ
指示線の矢で示す円筒面の半径方向の振れは、データム軸直線A-Bに関して一回転させたときに、デー . エピポーラ幾何 (Epipolar Geometry) | CVMLエキスパートガイド. 1. エピポーラ幾何 (Epipolar Geometry)とは [概要] エピポーラ幾何 (Epipolar Geometry)とは,ステレオビジョンにおける2カメラ間での幾何のことである.同一物体・シーンを,異なる2箇所・(2方向) から同一シーンを撮影した際に,カメラ中心2つとシーン中の1点の間で必ず発生する「幾何的拘束( =エピ . ペプチド結合 - 近畿大学理工学部 理学科 化学コース / 理学専攻 . ペプチド結合. 図 ポリペプチド主鎖の回転角(φ、ψ). 読み方 φ:ファイ、 ψ:プサイ. peptide.ppt アニメーション (パワーポイント) C-Nの二重結合性のため6個の原子(C-CO-NH-C)は同一平面上に存在する。. ⇒点線の四角で表される。. 点線の四角はそれぞれの . 【入門線形代数】一次独立・一次従属とは?-ベクトル空間-. 「一次独立・一次従属とは?」では,ベクトル空間を考えるうえでとても重要な概念である,一次独立と一次従属について勉強します. 後に学習していくとわかることですが,この一次独立と一次従属は集合の広がり度合いを調べることができるものです